Notes: Probability

Basics

Let

{A}

be an event.

{P(A)}

represents the probability that

{A}

occurs.

{0 \leq P(A) \leq 1}

for any event

{A.}

{P(A) =0}

if no outcomes are possible for

{A}

.

{P(A) =1}

if

{A}

contains all possible outcomes.

If

{A}

is a subset of

{B}

(i.e.

{A \subseteq B}

), then

{P(A) \leq P(B).}

Notation

Complement

{P(A')}

: probability of not

{A}

.

Intersection

{P(A\cap B)}

: probability of

{A}

and

{B}

.

Union

{P(A\cup B)}

: probability of

{A}

or

{B}

(or both).

Conditional probability

{P(A \mid B)}

: probability of

{A}

given that

{B}

has occurred.

Formula summary

{P(A')=1-P(A)}

P(A \mid B)=\frac{P(A \cap B)}{P(B)}

{P(A \cup B)} \allowbreak {=P(A)+P(B)-P(A\cap B)}

Adding and multiplying probabilities

Let

{A}

be made up of either case 1 or case 2 with individual probabilities

{p_1}

and

{p_2}

. If they do not overlap, then the probability of

{A}

is given by

{p_1+p_2.}

Let

{A}

be made up of step 1 with probability

{p_1}

followed by step 2 with conditional probability

{p_2}

. Then the probability of

{A}

is given by

{p_1p_2.}

Conditional probabilities

Probabilities "change" depending on the information we have.

For example, consider a box with 4 red balls and 2 green balls from which we draw without replacement. Let

{A}

be the event that we draw a green ball on the second draw and

{B}

be the event we draw a red ball on the first draw.

If we knew that we have drawn a red ball on the first draw, then the probability of ending up with a green ball on the second draw,

{P(A \mid B) = \frac{2}{5}.}

If we knew that we have drawn a green ball on the first draw, then the probability of ending up with a green ball on the second draw is

{P(A \mid B') = \frac{1}{5}.}

Meanwhile,

{P(A \cap B) = \frac{4}{6} \times \frac{2}{5} = \frac{4}{15}}

and

{P(A) = \frac{4}{15}+\frac{2}{6}\times \frac{1}{5}=\frac{1}{3}.}

\boxed{P(A \mid B)=\frac{P(A\cap B)}{P(B)}}

A tree diagram can be very useful in visualizing situations with multiple steps.

Example 1: tree diagram

There is a probability of 0.6 that Daniel takes his parents' car to go to school. Otherwise, he will take a bus.

If he takes his parents' car, he has a 0.01 probability of being late. The probability that Daniel is late for school if he took a bus is 0.05.

Find the probability that

(a) Daniel arrives to school on time,

(b) Daniel took the bus, given that he was late for school.

On two randomly chosen days, find the probability that

(c) Daniel was late exactly once.

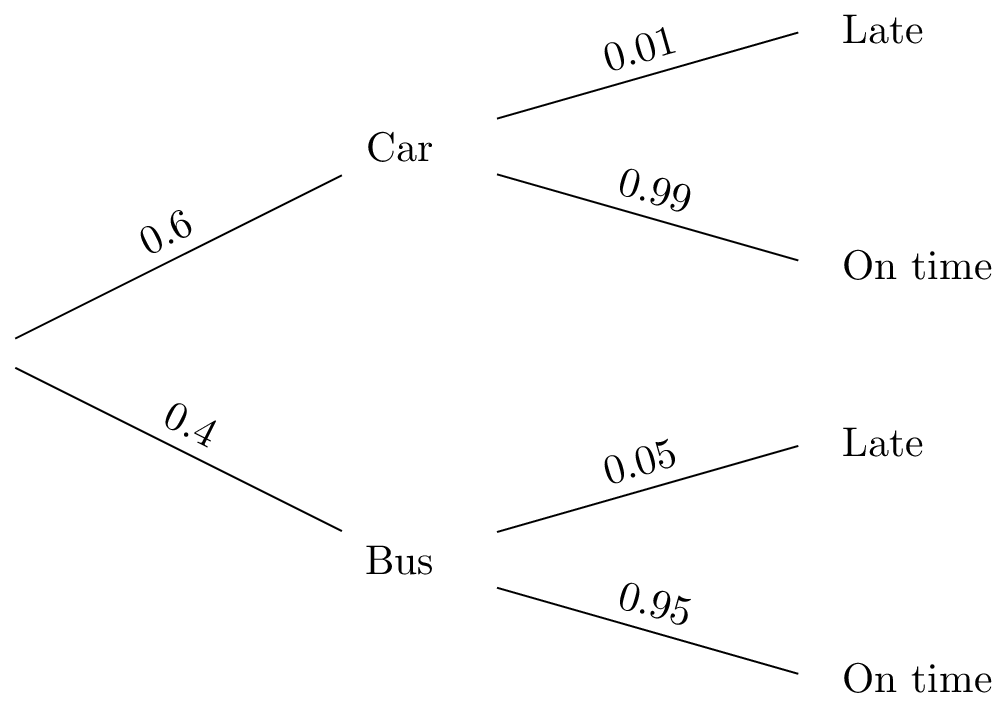
(a) Probability required

{=0.6\times 0.99 + 0.4 \times 0.95} \allowbreak {= 0.974.}

(b)

\displaystyle {P(\textrm{bus} \mid \textrm{late}}) \allowbreak {= \frac{P(\textrm{bus} \cap \textrm{late})}{P(\textrm{late})}} \allowbreak {= \frac{0.4\times 0.05}{1-0.974}} {= \frac{10}{13}.}

(c) Probability required

{= 0.974 \times (1-0.974) \times 2!} \allowbreak {= 0.0506.}

Venn diagrams

Venn diagram are very useful in visualizing sets, especially those involving complements, unions and/or intersections.

The union formula

When tackling either/or type of events that overlap, the union formula allows us to break our analysis into simpler events.

P(A\cup B) \allowbreak {= P(A)+P(B)-P(A \cap B)}

Example 2: Venn diagram

Two events

{A}

and

{B}

are such that

{P(A)=0.7,}

{P(B)=0.5,}

and

{P(A \cap B')=0.38.}

Find the value of

(a)

{P(A \cup B),}

(b)

{P(A' \mid B').}

(a)

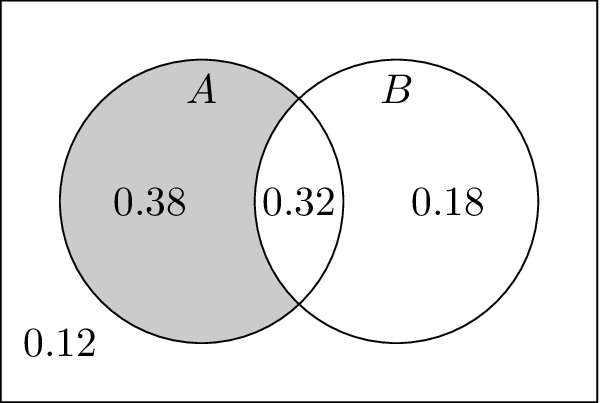
{P(A \cup B) } \allowbreak {=0.38+0.5=0.88.}

(b)

\displaystyle P(A' \mid B') \allowbreak {= \frac{P(A' \cap B')}{P(B')}} \allowbreak {= \frac{0.12}{1-0.5} = 0.24.}

Permutations and combinations

Probabilities can be calculated by counting the number of ways:

\displaystyle P(A) \allowbreak =\frac{\textrm{number of ways for }A}{\textrm{total number of ways}}

Example 3: permutations and combinations

Anna has 7 blouses, 3 skirts and 6 accessories, all distinct. One blouse has a floral pattern while another has a polka dot design.

(a) Anna hangs all her blouses in a line. Find the probability that the floral blouse is next to the polka dot blouse.

For Anna, an outfit consists of one blouse, one skirt and either one or two accessories and wears them.

(b) Find the total number of unique outfits that Anna has.

Anna picks an outfit randomly such that each unique outfit has the same chance of being chosen.

(c) Find the probability that her outfit today consists of either her floral blouse or exactly two accessories (or both).

(a)

{\frac{6! \times 2!}{7!}=\frac{2}{7}}

(b)

\binom{7}{1}\times\binom{3}{1}\times \left( \binom{6}{1} + \binom{6}{2} \right) \allowbreak {=441}

(c)

{\frac{1\times\binom{3}{1}\times\left(\binom{6}{1}+\binom{6}{2}\right)}{441}} \allowbreak + \allowbreak {\frac{\binom{7}{1}\times\binom{3}{1}\times\binom{6}{2}}{441}}\allowbreak -\allowbreak {\frac{1\times\binom{3}{1}\times\binom{6}{2}}{441}} \allowbreak {=\frac{37}{49}}

Mutually exclusive events

Two events

{A}

and

{B}

are mutually exclusive if they cannot occur at the same time.

P(A\cap B)=0 \allowbreak {\quad \textrm{ if } A,B \textrm{ mutually exclusive}}

Example: "heads on a coin flip" and "tails on the same coin flip"

Independent events

P(A\cap B)=P(A) \cdot P(B) \allowbreak {\quad \textrm{ if } A,B \textrm{ independent}}

Intuitively,

{A}

and

{B}

are independent if

{A}

does not "affect" the probability of

{B}

(and vice versa).

Alternatively,

{P(A\mid B) = P(A)}

if

{A,B}

independent.

Example: "heads on the first coin flip" and "tails on the second coin flip"

Example 4: table of outcomes

Two fair dice, one blue and one red, are thrown. Let

{A}

denote the event that the blue die shows a 2. Let

{B}

denote the event that the sum of the two dice is 7.

(a) Find the probability that either

{A}

or

{B}

occurs (but not both).

(b) Are the events

{A}

and

{B}

mutually exclusive?

(c) Are the events

{A}

and

{B}

independent?

Sum	1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

(a)

{\frac{10}{36}=\frac{5}{18}}

(b) No, since

{P(A \cap B) = \frac{1}{36} \neq 0}

(c)

{P(A \cap B)=\frac{1}{36}}

{P(A) \cdot P(B)=\frac{6}{36}\cdot \frac{6}{36} = \frac{1}{36}}

Since

{P(A \cap B) = P(A) \cdot P(B),}

they are independent.

Example 5: exam style question (tree diagram)

To predict the weather, a simple computer simulation uses the following model:

The probability that it rains on the first day is 0.6. For the next two days, the probability of rain is

0.1 higher than the probability of raining the previous day if it rained the previous day,

half the probability of raining the previous day if it did not rain the previous day.

(a) Find the probability that it rains on all three days.

(b) Find the probability that it rained on at least one day.

(c) Find the probability that it rained on the first day, given that it rained on the third day.

(a)

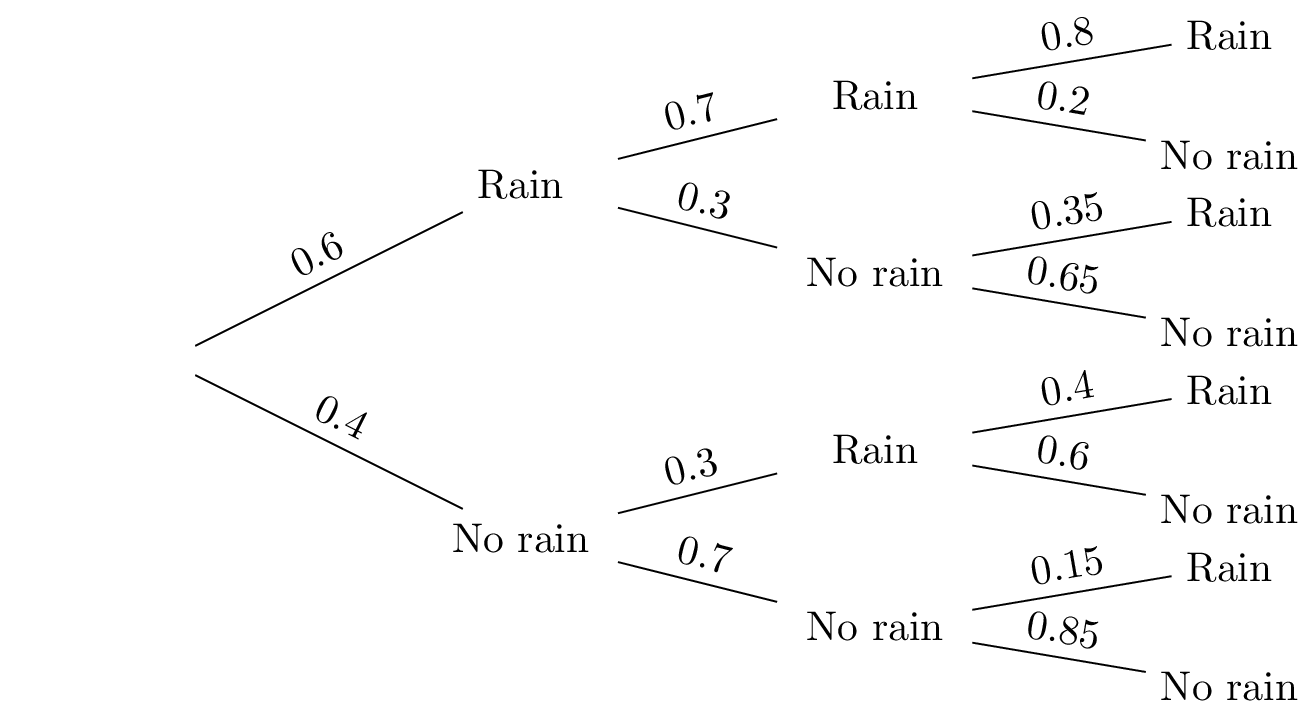
{0.6\times 0.7\times 0.8 = 0.336.}

(b)

{1-0.4\times 0.7 \times 0.85 = 0.762.}

(c)

P(\textrm{rain first}\cap \textrm{rain third})\allowbreak {=0.336+0.6\times 0.3\times 0.35} \allowbreak {= 0.399}

P(\textrm{rain third})\allowbreak {=0.399+0.4\times 0.3 \times 0.4} \allowbreak {+0.4\times 0.7 \times 0.15} \allowbreak {= 0.489}

\displaystyle P(\textrm{rain first} \mid \textrm{rain third}) \allowbreak {= \frac{0.399}{0.489}=0.816.}

Example 6: range of probabilities

Two events

{A}

and

{B}

are such that

{P(A)=0.6}

and

{P(B)=0.7}

Find the range of possible values of

{P(A\cap B).}

Let

{P(A\cap B)}

be

{x.}

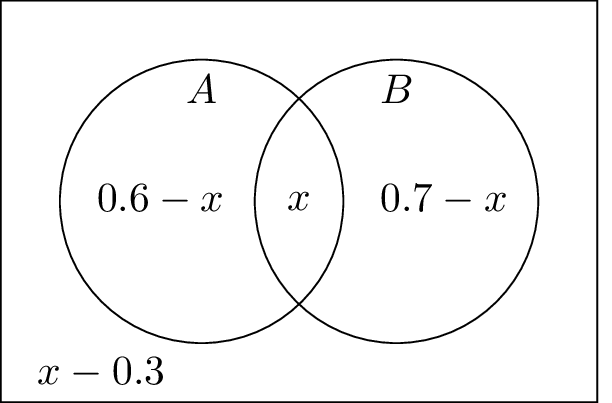
Since all probabilities must be between 0 and 1,

{0.3 \leq P(A \cap B) \leq 0.6.}

Example 7: exam style question (venn diagram)

Events

{A}

and

{B}

are such that

{P(A)=0.6,}

{P(B)=0.9}

and

{P(A \cap B)=0.59}

(a) Find

{P(A\cup B).}

For a third event

{C}

it is given that

{P(C)=0.7}

and that

{A}

and

{C}

are independent.

(b) Find

{P(A'\cap C)}

(c) Find the range of possible values of

{P(A'\cap B \cap C)}

(a)

{0.6+0.9-0.59=0.91.}

(b)

{(1-0.6) \times 0.7 = 0.28.}

(c)

{0.19 \leq P(A' \cap B \cap C) \leq 0.28.}